Quantum Monte Carlo | Werner Dobrautz

Instead of describing all possible states of a system, Monte Carlo (MC) methods rely on random numbers to sample the physically most relevant and representative ones and draw conclusions from them to understand the underlying physical properties of a system.

Full configuration interaction quantum Monte Carlo (FCIQMC) [1, 2, 3] is a QMC method to solve the Schrödinger equation of a system with very high accuracy and for comparatively large system sizes. It can obtain ground and excited states energies [4] , as well as static [5, 6] and dynamic properties[7] of ab initio problems, as well as lattice models, i.e., Hubbard [8] or Heisenberg Hamiltonians [9] .

The open-source repository of our FCIQMC code base NECI can be found here.

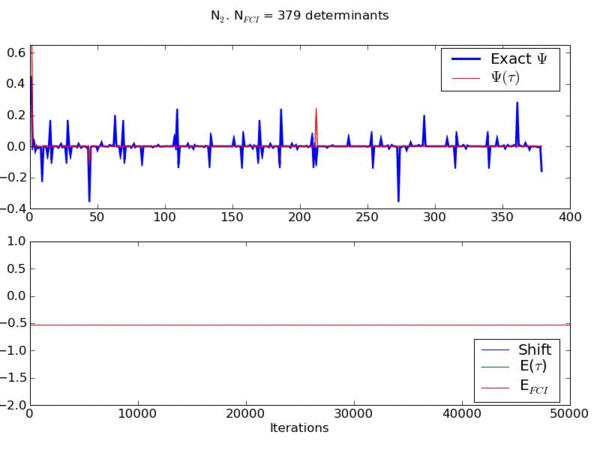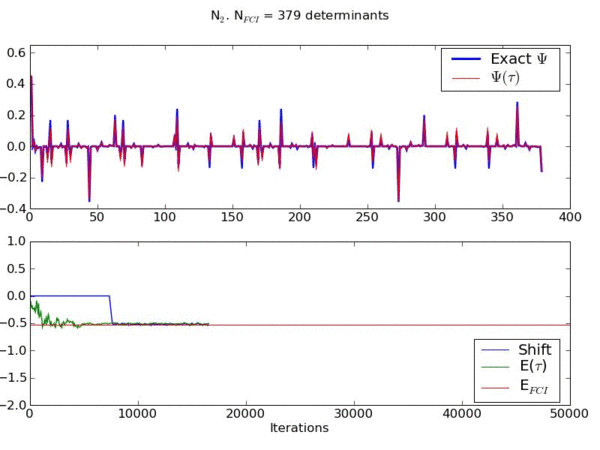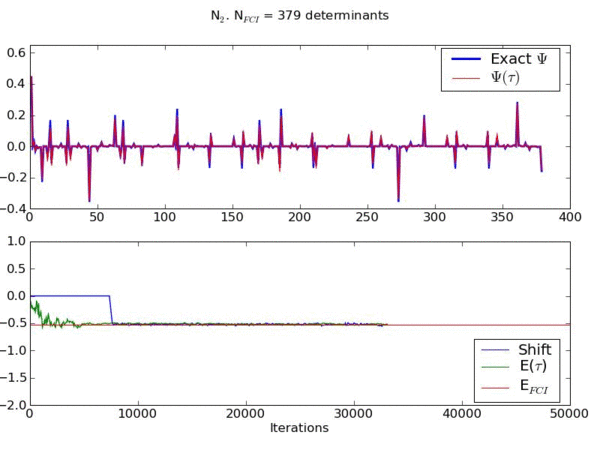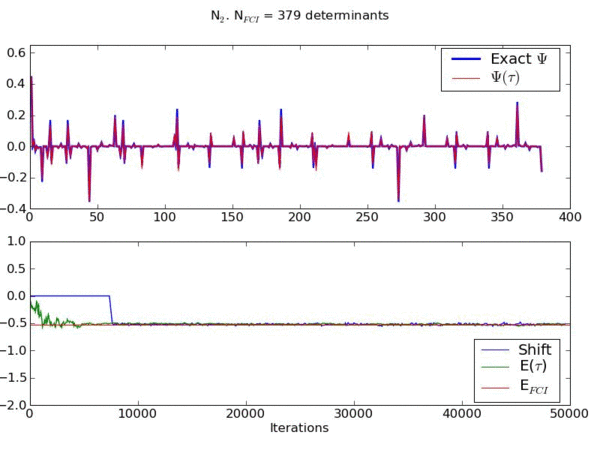
Example of an FCIQMC simulation for a model of streched N2 from http://www-alavi.ch.cam.ac.uk/

Related Publications:

2021

JCTC
Spin-Pure Stochastic-CASSCF via GUGA-FCIQMC Applied to Iron–Sulfur Clusters

Werner Dobrautz, Oskar Weser, Nikolay A. Bogdanov, Ali Alavi, and Giovanni Li Manni

Journal of Chemical Theory and Computation, Sep 2021

Abs arXiv Bib HTML

In this work, we demonstrate how to efficiently compute the one- and two-body reduced density matrices within the spin-adapted full configuration interaction quantum Monte Carlo (FCIQMC) method, which is based on the graphical unitary group approach (GUGA). This allows us to use GUGA-FCIQMC as a spin-pure configuration interaction (CI) eigensolver within the complete active space self-consistent field (CASSCF) procedure and hence to stochastically treat active spaces far larger than conventional CI solvers while variationally relaxing orbitals for specific spin-pure states. We apply the method to investigate the spin ladder in iron–sulfur dimer and tetramer model systems. We demonstrate the importance of the orbital relaxation by comparing the Heisenberg model magnetic coupling parameters from the CASSCF procedure to those from a CI-only (CASCI) procedure based on restricted open-shell Hartree–Fock orbitals. We show that the orbital relaxation differentially stabilizes the lower-spin states, thus enlarging the coupling parameters with respect to the values predicted by ignoring orbital relaxation effects. Moreover, we find that, while CASCI results are well fit by a simple bilinear Heisenberg Hamiltonian, the CASSCF eigenvalues exhibit deviations that necessitate the inclusion of biquadratic terms in the model Hamiltonian.
@article{Dobrautz2021, doi = {10.1021/acs.jctc.1c00589}, url = {https://doi.org/10.1021/acs.jctc.1c00589}, year = {2021}, month = sep, publisher = {American Chemical Society ({ACS})}, volume = {17}, number = {9}, pages = {5684--5703}, author = {Dobrautz, Werner and Weser, Oskar and Bogdanov, Nikolay A. and Alavi, Ali and Manni, Giovanni Li}, title = {Spin-Pure Stochastic-{CASSCF} via {GUGA}-{FCIQMC} Applied to Iron{\textendash}Sulfur Clusters}, journal = {Journal of Chemical Theory and Computation}, dimensions = {true}, project_guga = {true}, project_devel = {true}, project_tm = {true}, project_fciqmc = {true} }

2020

JCP
NECI: N-Electron Configuration Interaction with an emphasis on state-of-the-art stochastic methods

Kai Guther, Robert J. Anderson, Nick S. Blunt, Nikolay A. Bogdanov, Deidre Cleland, and 20 more authors

The Journal of Chemical Physics, Jul 2020

Abs arXiv Bib HTML

We present NECI, a state-of-the-art implementation of the Full Configuration Interaction Quantum Monte Carlo (FCIQMC) algorithm, a method based on a stochastic application of the Hamiltonian matrix on a sparse sampling of the wave function. The program utilizes a very powerful parallelization and scales efficiently to more than 24 000 central processing unit cores. In this paper, we describe the core functionalities of NECI and its recent developments. This includes the capabilities to calculate ground and excited state energies, properties via the one- and two-body reduced density matrices, as well as spectral and Green’s functions for ab initio and model systems. A number of enhancements of the bare FCIQMC algorithm are available within NECI, allowing us to use a partially deterministic formulation of the algorithm, working in a spin-adapted basis or supporting transcorrelated Hamiltonians. NECI supports the FCIDUMP file format for integrals, supplying a convenient interface to numerous quantum chemistry programs, and it is licensed under GPL-3.0.
@article{Guther2020, doi = {10.1063/5.0005754}, url = {https://doi.org/10.1063/5.0005754}, year = {2020}, month = jul, publisher = {{AIP} Publishing}, volume = {153}, number = {3}, pages = {034107}, author = {Guther, Kai and Anderson, Robert J. and Blunt, Nick S. and Bogdanov, Nikolay A. and Cleland, Deidre and Dattani, Nike and Dobrautz, Werner and Ghanem, Khaldoon and Jeszenszki, Peter and Liebermann, Niklas and Manni, Giovanni Li and Lozovoi, Alexander Y. and Luo, Hongjun and Ma, Dongxia and Merz, Florian and Overy, Catherine and Rampp, Markus and Samanta, Pradipta Kumar and Schwarz, Lauretta R. and Shepherd, James J. and Smart, Simon D. and Vitale, Eugenio and Weser, Oskar and Booth, George H. and Alavi, Ali}, title = {{NECI}: N-Electron Configuration Interaction with an emphasis on state-of-the-art stochastic methods}, journal = {The Journal of Chemical Physics}, dimensions = {true}, project_guga = {true}, project_devel = {true}, project_fciqmc = {true} }

2019

PhD Thesis
Development of Full Configuration Interaction Quantum Monte Carlo Methods for Strongly Correlated Electron Systems

Werner Dobrautz

University of Stuttgart, Mar 2019

Abs Bib HTML PDF

Full Configuration Interaction Quantum Monte Carlo (FCIQMC) is a prominent method to calculate the exact solution of the Schrödinger equation in a finite antisymmetric basis and gives access to physical observables through an efficient stochastic sampling of the wavefunction that describes a quantum mechanical system. Although system-agnostic (black-box-like) and numerically exact, its effectiveness depends crucially on the compactness of the wavefunction: a property that gradually decreases as correlation effects become stronger. In this work, we present two -conceptually distinct- approaches to extend the applicability of FCIQMC towards larger and more strongly correlated systems. In the first part, we investigate a spin-adapted formulation of the FCIQMC algorithm, based on the Unitary Group Approach. Exploiting the inherent symmetries of the nonrelativistic molecular Hamiltonian results in a dramatic reduction of the effective Hilbert space size of the problem. The use of a spin-pure basis explicitly resolves the different spin-sectors, even when degenerate, and the absence of spin-contamination ensures the sampled wavefunction is an eigenfunction of the total spin operator. Moreover, targeting specific many-body states with conserved total spin allows an accurate description of chemical processes governed by the intricate interplay of them. We apply the above methodology to obtain results, not otherwise attainable with conventional approaches, for the spin-gap of the high-spin cobalt atom ground- and low-spin excited state and the electron affinity of scandium within chemical accuracy to experiment. Furthermore we establish the ordering of the scandium anion bound states, which has until now not been experimentally determined. In the second part, we investigate a methodology to explicitly incorporate electron correlation into the initial Ansatz of the ground state wavefunction. Such an Ansatz induces a compact description of the wavefunction, which ameliorates the sampling of the configuration space of a system with FCIQMC. Within this approach, we investigate the two-dimensional Hubbard model near half-filling in the intermediate interaction regime, where such an Ansatz can be exactly incorporated by a nonunitary similarity transformation of the Hamiltonian based on a Gutzwiller correlator. This transformation generates novel three-body interactions, tractable due to the stochastic nature of FCIQMC, and leads to a non-Hermitian effective Hamiltonian with extremely compact right eigenvectors. The latter fact allows application of FCIQMC to larger lattice sizes, well beyond the reach of the method applied to the original Hubbard Hamiltonian.
@phdthesis{dobrautz-phd, title = {Development of Full Configuration Interaction Quantum Monte Carlo Methods for Strongly Correlated Electron Systems}, author = {Dobrautz, Werner}, school = {University of Stuttgart}, year = {2019}, month = mar, url = {http://dx.doi.org/10.18419/opus-10593}, doi = {10.18419/opus-10593}, project_devel = {true}, project_fciqmc = {true}, project_guga = {true}, project_tc = {true}, project_thesis = {true}, owner = {dobrautz}, timestamp = {2019.04.16} }
JCP
Efficient formulation of full configuration interaction quantum Monte Carlo in a spin eigenbasis via the graphical unitary group approach

Werner Dobrautz, Simon D. Smart, and Ali Alavi

The Journal of Chemical Physics, Sep 2019

Abs arXiv Bib HTML

We provide a spin-adapted formulation of the Full Configuration Interaction Quantum Monte Carlo (FCIQMC) algorithm, based on the Graphical Unitary Group Approach (GUGA), which enables the exploitation of SU(2) symmetry within this stochastic framework. Random excitation generation and matrix element calculation on the Shavitt graph of GUGA can be efficiently implemented via a biasing procedure on the branching diagram. The use of a spin-pure basis explicitly resolves the different spin-sectors and ensures that the stochastically sampled wavefunction is an eigenfunction of the total spin operator Ŝ 2⁠. The method allows for the calculation of states with low or intermediate spin in systems dominated by Hund’s first rule, which are otherwise generally inaccessible. Furthermore, in systems with small spin gaps, the new methodology enables much more rapid convergence with respect to walker number and simulation time. Some illustrative applications of the GUGA-FCIQMC method are provided: computation of the 2F − 4F spin gap of the cobalt atom in large basis sets, achieving chemical accuracy to experiment, and the Σg+1⁠, Σg+3⁠, Σg+5⁠, and Σg+7 spin-gaps of the stretched N2 molecule, an archetypal strongly correlated system.
@article{Dobrautz2019, doi = {10.1063/1.5108908}, url = {https://doi.org/10.1063/1.5108908}, year = {2019}, month = sep, publisher = {{AIP} Publishing}, volume = {151}, number = {9}, author = {Dobrautz, Werner and Smart, Simon D. and Alavi, Ali}, title = {Efficient formulation of full configuration interaction quantum Monte Carlo in a spin eigenbasis via the graphical unitary group approach}, journal = {The Journal of Chemical Physics}, dimensions = {true}, project_guga = {true}, project_devel = {true}, project_fciqmc = {true} }

2018

PRL
Time Propagation and Spectroscopy of Fermionic Systems Using a Stochastic Technique

Kai Guther, Werner Dobrautz, Olle Gunnarsson, and Ali Alavi

Phys. Rev. Lett., Aug 2018

Abs arXiv Bib HTML

We present a stochastic method for solving the time-dependent Schrödinger equation, generalizing a ground state full configuration interaction quantum Monte Carlo method. By performing the time integration in the complex plane close to the real-time axis, the numerical effort is kept manageable and the analytic continuation to real frequencies is efficient. This allows us to perform ab initio calculation of electron spectra for strongly correlated systems. The method can be used as a cluster solver for embedding schemes.
@article{PhysRevLett.121.056401, title = {Time Propagation and Spectroscopy of Fermionic Systems Using a Stochastic Technique}, author = {Guther, Kai and Dobrautz, Werner and Gunnarsson, Olle and Alavi, Ali}, journal = {Phys. Rev. Lett.}, volume = {121}, issue = {5}, pages = {056401}, numpages = {5}, year = {2018}, month = aug, publisher = {American Physical Society}, doi = {10.1103/PhysRevLett.121.056401}, url = {https://link.aps.org/doi/10.1103/PhysRevLett.121.056401}, dimensions = {true}, project_devel = {true}, project_fciqmc = {true} }